Сотрудники международного научно-исследовательского центра по теоретическому материаловедению (МНИЦТМ) доказали, что топологический подход (с его помощью описывают и прогнозируют способы превращения химических объектов - атомов, молекул, кластеров - в более сложные архитектуры) может быть вполне эффективен при анализе атомных подрешеток в боридах, карбидах, нитридах и силицидах металлов.
Свои наблюдения ученые описали в журнале Королевского химического общества CrystEngComm (doi: 10.1039/D4CE01009D). Статью включили в список наиболее интересных статей, опубликованных за последний квартал.
"Мы показали, что топологический подход может быть применен не только к связанным частям кристаллических структур, но и к атомным подрешеткам, которые обычно анализируются как наборы точек геометрическими методами", - рассказывает старший научный сотрудник МНИЦТМ Инна Медриш.
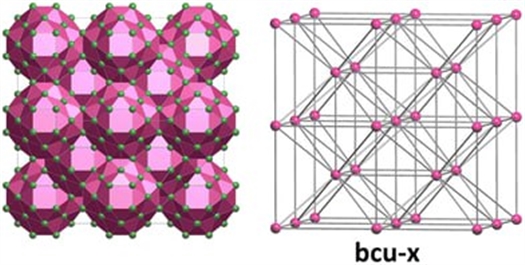
Ученые проанализировали топологические типы - тот "рисунок", который образует "периодическая сетка".
Изучены целые кристаллические структуры и несвязанные неметаллические подрешетки. В итоге команда пришла к выводу, что даже геометрически искаженные мотивы (причин искажений может быть много: химическая природа атомов, условия синтеза, последующее воздействие на вещество давлением и/или температурой и пр.) могут быть отнесены к одному и тому же типологическому типу, одновременно могут быть найдены связи между различными типами структур. Это важное преимущество предлагаемого подхода. Более того, возможные симметрии искаженных мотивов могут быть предсказаны на основе наиболее симметричной подрешетки.
Для оценки искажения подрешетки ученые предложили новый параметр, который также можно рассматривать как меру однородности подрешетки.
"Предположим, вещество образовано двумя сортами атомов: металлом и неметаллом, - поясняет Инна Медриш. - Все атомы в структуре образуют кристаллическую решетку, а отдельно взятые атомы (металла или неметалла) - подрешетки. Мы рассматривали частный случай, когда подрешетка образована из несвязанных друг с другом атомов неметаллов. Такая подрешетка будет однородной (или равномерной), если все образующие ее атомы находятся друг от друга на одинаковом расстоянии".
Политеховские ученые выяснили, что в большинстве случаев подрешетки неметаллических атомов обладают высокой однородностью. Это объясняется тем, что отрицательно заряженные атомы располагаться как можно дальше друг от друга. Критерий однородности может быть использован для суждения о структурной роли атомов подрешетки, которые могут предопределять архитектуру всего вещества.



















Последние комментарии
... будущим оперативным ДИРЕКТОРАМ - ЕСТЬ наработки технических решений ПРОЛЁТНОГО транспорта; ... приглашаю ЗАИНТЕРЕССАНТОВ на совместную разработку ... pestrikov_y@mail.ru
В области талантливых ребят достаточно много, такие мероприятия нужно поставить на поток.
Дело нужное. Хрупкий материал...
9 и 11классы не белеют?
Как показывает время, ничего эффективнее номерков на руке не придумали. Гоните директора, чему он современных детей научит, судя по организации набора в школу